1. Suppose there is a Kripke Structure S for the modal logic of knowledge that satisfies the following conditions:
(a) Represent the last condition above using formal notation.
(b) Draw S.
2. Consider the situation where there are two agents who each flip a coin. The outcome can be represented the proposition H1 to mean "Agent 1 got heads" (therefore ~H1 means "Agent 1 got tails") and H2 to mean "Agent 2 got heads" (therefore ~H2 means "Agent 2 got tails"). Draw a Kripke Structure that contains worlds for each possible outcome, where each agent knows the result of his own flip but not the result of the other agent's flip.
3. A Quasigroup of Order N is an N x N grid, where each cell contains an integer in the range 1 to N, and no integer is repeated in any row or column. Write propositional schema that has the property that every model of the instantiated schema corresponds to a quasigroup and every quasigroup corresponds to a model.
Hint for final exam: How do quasigroups relate to Sudoko?
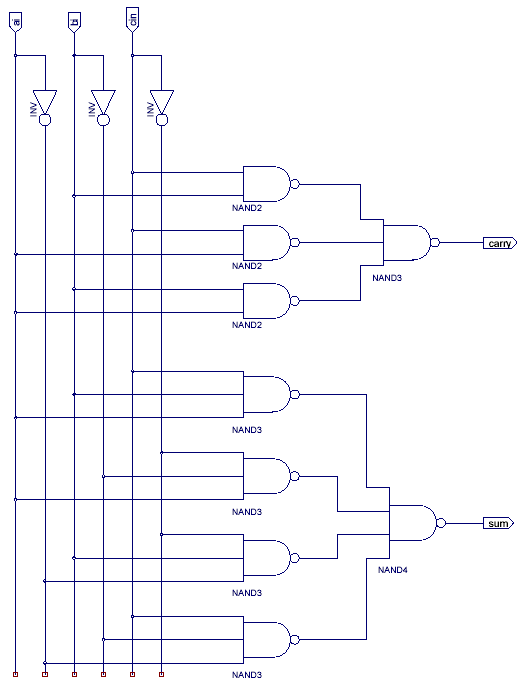
4. Describe how a consistency-based diagnostic system that uses Default Logic could be used to test and locate faults in implementations of the following circuit for a 1-bit adder. Your description should state the axioms and rules needed. You can assume that any of the nand or inverter gates could be faulty, but all of the wires are okay.

5. Although determining if a propositional formula is NP-complete in general, it can done in polynomial (in fact, linear) time if the formula is Horn (contains at most one positive literal per clause), or if the formula only consists of binary (two literal) clauses. If the formula is allowed to contain both Horn clauses and all-positive binary clauses, however, the problem becomes NP-complete again. Prove this by describing a general method for translating an arbitrary CNF formula into one containing only Horn and binary clauses, where the translation preserves satisfiability (i.e., the translated formula is satisfiable if and only if the original formula is satisfiable). Hint: your translation will need to introduce new propositions.
6. Write a Prolog program that finds a solution to the following puzzle.
1. There are three houses in a row on street. Each house is inhabited by a man of a different nationality, who has a different pet, and drinks a different beverage.
2. The Spaniard own a dog.
3. The Ukranian drinks tea.
4. The man in the third house drinks milk.
5. The Norwegian lives next to the tea drinker.
6. The juice drinker owns a fox.
7. The fox is next door to the dog.
Question: For each house: who lives there, what pet does he have, and what does he drink?
Notes: In Prolog, the atom "X=Y" is true if X and Y unify. The atom "X\=Y" is true if X and Y do not unify. A good way to solve the puzzle is write a clause that guesses at a complete solution, and then verifies that it is correct. Use terms to represent each house, and predicates such as house(H), next(H1,H2), milk(H), juice(H), etc.
7. Translate the following into FOL.
Seniors attend graduation.
Either Mary or Tom are seniors.
Use resolution refutation to answer the question: Will someone attend graduation? Use resolution refutation with answer extraction to try to answer the question: Who will attend graduation? Explain why no answer is returned. Add the assertion "John is a senior". Now show how answer extraction can succeed.
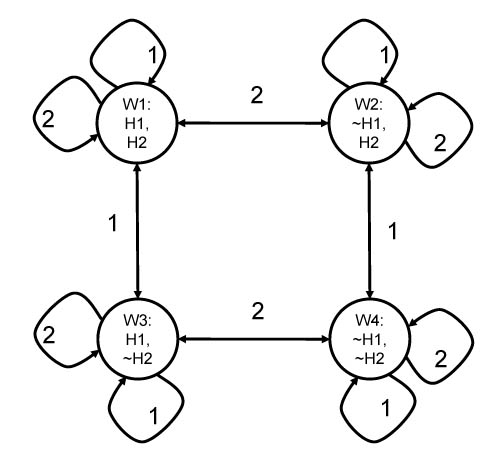
1. (a) <S,w1> |= (K1 p) & (K2 p) & (K1 K2 p) & (~K2 K1 p)
(b) 
2.